José María Arias Cabezas e Ildefonso Maza Sáez autores de Bruño de ESO y Bachillerato

Aunque muchos libros de Primaria y Secundaria dicen que el número 1 es primo, esto no es cierto.

1. Divisibilidad en los números naturales

Definición: Un número es primo si tiene exactamente dos divisores; el 1 y él mismo.

El número 1 no es primo porque solo tiene un divisor.

    Ejemplos de números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23, ...

Definición: Un número distinto de cero es compuesto si tiene más de dos divisores.

El número 1 no es compuesto porque solo tiene un divisor.

    Ejemplos de números compuestos: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21...

Por tanto, el número 1, no es ni primo ni compuesto.

El 1 es una unidad porque divide a todos los números naturales.

2. Anillos

En realidad, la divisibilidad se define en un anillo, por ello solo se habla de divisibilidad en el anillo de los números enteros y en el anillo de lo polinomios. También se habla de divisibilidad en los números naturales aplicando criterios análogos a los de los números enteros.

En un anillo, se dice que un elemento es una unidad si divide a todos los demás elementos del anillo. Así que en el anillo de los números enteros son unidades el 1 y el - 1

3. Divisibilidad en los números enteros

Definición: Un número a es primo si tiene exactamente cuatro divisores; el ± 1 y ± a

    Ejemplos de números primos: ± 2, ± 3, ± 5, ± 7, ± 11, ± 13, ± 17, ± 19, ± 23, ...

Definición: Un número distinto de cero es compuesto si tiene más de cuatro divisores.

    Ejemplos de números compuestos: ± 4, ± 6, ± 8, ± 9, ± 10, ± 12, ± 14, ± 15, ± 16, ± 18, ± 20, ± 21...

4. Divisibilidad en los números racionales, reales y complejos

En los números racionales, reales y complejos no tiene sentido hablar de divisibilidad porque todos los números excepto el cero dividen a todos los números.

Ejemplo:

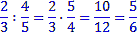Cada uno de estos conjuntos de números tiene estructura de cuerpo.

5. Divisibilidad en los polinomios y en las fracciones algebraicas

El conjunto de los polinomios tienen estructura de anillo y por ello también tiene sentido hablar de divisibilidad, sin embargo, el conjunto de las fracciones algebraicas tiene estructura de cuerpo y no tiene sentido hablar de divisibilidad.

Resumen: Solo se habla de divisibilidad en los números naturales y enteros; y en los polinomios.

La divisibilidad tiene aplicación:

a) A la suma y resta de fracciones numéricas y algebraicas.

b) En la simplificación de fracciones.

c) Para resolver algunos tipos de problemas numéricos.