
8. Polígonos, circunferencia y círculo
Introducción: ¿Para qué sirven los polígonos, la circunferencia y el círculo?
Los polígonos, la circunferencia y el círculo se utilizan frecuentemente en nuestra vida cotidiana y también sirven para aprender a pensar y razonar. En los años posteriores sirven para seguir estudiando y profundizando en Ciencia, Tecnología, Ingeniería y Matemáticas (CTIM)
Por ejemplo: Las medidas oficiales de una pista de pádel son 20 m ´ 10 m

Problema: Halla la superficie de una pista de pádel son 20 m ´ 10 m
Datos:
Pista de pádel rectangular de 20 m ´ 10 m
Pregunta:
Halla el área.
Planteamiento y operaciones:
La fórmula del área de un rectángulo es: A = b ´ a
Área = 20 ´ 10 = 200
Solución:
Área = 200 m²
8.1. Polígonos: Definiciones
Un polígono es la región de plano limitada por una línea poligonal cerrada.
Los elementos característicos de los polígonos son:
| Nombres | Figura |
| Lado |
 |
| Vértice |
 |
| Diagonal |
 |
| Apotema |
 |
Nombres de los polígonos
| Nombres | Figura |
| Triángulo |
 |
| Cuadrado |
 |
| Rectángulo |
 |
| Rombo |
 |
| Romboide |
 |
| Trapecio |
 |
| Trapezoide |
 |
Nombres de los polígonos regulares
Un polígono es regular si tiene sus lados y sus ángulos iguales.
| Nombres | Figura |
| Triángulo equilátero |
 |
| Cuadrado |
 |
| Pentágono |
 |
| Hexágono |
 |
| Heptágono |
 |
| Octógono |
 |
| Eneágono |
 |
| Decágono |
 |
APLICA LA TEORÍA: CUADERNO
1. Dibuja un triángulo y un rombo. 2. Dibuja un rectángulo y un romboide. 3. Dibuja un pentágono regular y un hexágono regular.8.2. Polígonos: Perímetros y áreas
El perímetro de un polígono es la medida de su contorno y se calcula sumando las longitudes de los lados.| Nombre | Perímetro | Ejemplo | Área | Ejemplo |
| Triángulo | El perímetro de un triángulo es igual a la suma de sus 3
lados.
P = a + b + c ¡Ojo! a es un lado |
 |
El área de un triángulo es igual a la base multiplicada por
la altura y dividido entre dos.
¡Ojo! a es la altura |
 |
| Cuadrado | El perímetro de un cuadrado es igual a 4 veces el lado.
P = 4a |
 |
El área de un cuadrado es igual al lado al cuadrado.
A = a² |
 |
| Rectángulo |
El perímetro de
un rectángulo es
igual al doble de la base más la altura, ya que tiene dos lados
iguales. P = 2(b + a) |
 |
El área de un rectángulo es igual a la base por la altura.
A = b · a |
 |
| Rombo | El perímetro de un rombo es igual a 4 veces el lado.
P = 4a |
 |
El área de un rombo es igual a la diagonal mayor por la
diagonal menor y dividido entre dos.
|
 |
| Romboide | El perímetro de un romboide es igual al doble de la suma de
dos lados contiguos.
P = 2(b + a) ¡Ojo! a es un lado |
 |
El área de un romboide es igual a la base por la altura.
A = b · a ¡Ojo! a es la altura |
 |
| Trapecio | El perímetro de un trapecio es igual a la suma de los lados.
P = B + b + c + d |
 |
El área de un trapecio es igual a la semisuma de las bases
por la altura.
|
 |
| Trapezoide y figuras irregulares |
El perímetro de un trapezoide es igual a la suma de los lados.
P = B + b + c + d Cualquier figura irregular se puede descompone en suma de figuras conocidas. |
 |
El área de un trapezoide es igual a la suma de las áreas de los dos triángulos. | |
| Polígono regular | El perímetro de un polígono regular es igual al número de
lados multiplicado por lo que mide cada lado.
P = n · l |
 |
El área de un polígono regular es igual al perímetro
multiplicado por la apotema y dividido entre dos.
|
 |
APLICA LA TEORÍA: CUADERNO
1.
Calcula el perímetro y el área de un rectángulo de base 8,2 m y altura 3,5 m2. Calcula el perímetro y el área de un trapecio de bases 9,2 m, 5,8 m y altura 4,3 m
3. Calcula el perímetro y el área de la siguiente figura:
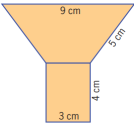
8.3.Circunferencia y círculo: Definiciones
Una circunferencia es una línea curva, cerrada y plana cuyos puntos están a la misma distancia de un punto fijo llamado centro.
Un círculo es la parte del plano limitada por una circunferencia.| Circunferencia y sus elementos | Círculo y sus elementos | |||
| Circunferencia |
 |
Círculo |
 |
|
| Centro |
 |
Sector circular |
 |
|
| Radio |
 |
Segmento circular |
 |
|
| Cuerda |
 |
Corona circular |
 |
|
| Diámetro |
 |
Trapecio circular |
 |
|
| Semicircunferencia |
 |
|||
| Arco |
 |
|||
APLICA LA TEORÍA: CUADERNO
1. Dibuja una circunferencia y un diámetro.
2. Dibuja un círculo y un sector circular.
8.4. Circunferencia y círculo: Longitudes y áreas
La longitud de una circunferencia es la medida de su contorno.
| Nombre | Longitud | Ejemplo | Área | Ejemplo |
| Circunferencia | La longitud de una circunferencia es igual a 2 por π y multiplicado
por el radio.
L = 2πR, π se redondea habitualmente a 3,14 y en cálculo mental a 3
La longitud de una circunferencia es un poco más de tres veces el diámetro.
|
 |
||
| Círculo | El área del círculo es igual a π, multiplicado por el radio al
cuadrado.
A = πR², π se redondea habitualmente a 3,14 y en cálculo mental a 3 |
 |
Circunferencia y círculo: Longitudes y áreas
APLICA LA TEORÍA: CUADERNO
1.
Calcula la longitud de una circunferencia de radio 5 m2. Calcula el área de un círculo de radio 8 m
3. Calcula el perímetro y el área de la siguiente figura de dentro del cuadrado:

8.5. Problemas de polígonos, circunferencia y círculo
Procedimiento de resolución de problemas con planteamiento: Teoría
Para resolver un problema, debes leer varias veces el enunciado hasta que entiendas muy bien cuáles son los datos, las preguntas y las relaciones.
Este procedimiento se puede sintetizar en los siguientes pasos:
1. Datos
Lee bien el enunciado
2. Pregunta/s
3. Planteamiento y operaciones
4. Solución
Problema resuelto con los 4 pasos
Queremos poner césped natural en una plaza circular de radio 10 m, si el metro cuadrado de césped cuesta 5 €/m². ¿Cuánto cuesta el césped necesario?
1. Datos
Plaza circular de 10 m de radio.
Pecio del metro cuadrado de césped: 5 €/m²
2. Pregunta
¿Cuánto cuesta el césped necesario?
3. Planteamiento y operaciones
A = πR², π se redondea a 3,14
A = 3,14 · 5² = 3,14 · 25 = 78,5 m²
Coste = 78,5 · 5 = 392,5 €
4. Solución
Costo total: 392,5 €
Procedimiento de resolución de problemas para pensar y razonar: Teoría
Lo más importante en la resolución de problemas es aprender a pensar y razonar bien. Cuando ya tenemos soltura en el procedimiento de resolución de problemas con planteamiento, tenemos un cuestionario con 5 problemas en los que el objetivo es exclusivamente elegir o identificar la operación correcta. Así mejoramos nuestra agilidad y rapidez en la resolución de problemas.
Procedimiento de resolución de problemas para resolver mentalmente: Teoría
Cuando ya somos hábiles en el procedimiento de resolución de problemas con planteamiento y sabemos elegir rápidamente la operación matemática adecuada, es el momento de dar un paso más: Resolver problemas mentalmente sin necesidad de hacer todos los pasos. Para ello, tenemos un cuestionario con 5 problemas en los que tenemos que elegir la operación y hacer el cálculo mentalmente. Siempre el cálculo se puede hacer mentalmente, porque el objetivo es aprender a pensar y razonar sin complicarse con operaciones largas y difíciles.
IA (Inteligencia artificial): Teoría
En la parte superior, antes del Tema 1, tenemos las 3 Apps más importantes de Inteligencia Artificial (IA) para resolver 5 problemas del mismo estilo que has resuelto mentalmente.
Puedes utilizar la que más te guste y resolver los 5 problemas del cuestionario. Para resolver cada problema, lo más sencillo es copiar el enunciado de Moodle, pegarlo en la App y escribir el resultado en Moodle.
El objetivo es aprender a usar la IA, porque a partir de ahora la utilizaremos en muchas ocasiones en nuestra vida diaria.
Nota 1: Las Apps actuales de IA no son perfectas, por lo que es posible que el resultado de alguno de los problemas no sea correcto. Sin embargo, en el nivel de Educación Primaria, suelen resolver los problemas correctamente.
Nota 2: Cuando termines de hacer el cuestionario de 5 problemas de IA, compara el tiempo que has tardado con el tiempo que has utilizado en el cuestionario de resolución mentalmente, si eres rápido en pensar, razonar y calcular ¡le puedes ganar a la IA!
Nota 3: Al igual que cuando el profesor o profesora te manda hacer problemas y en alguno de ellos tienes dificultades para resolverlo, puedes comentarlo con un compañero para intentar resolverlo juntos. Del mismo modo, después de haberlo intentado por tu cuenta, puedes usar una App de IA que te explicará el problema con todo detalle. Recuerda que si copias un problema de un compañero o de la IA, sin intentar resolverlo, no aprenderás nada en absoluto.